PECVD-processen vinden plaats in een proceskamer die onder vacuüm staat, bij drukken van ongeveer 0,1 Pa tot 100 Pa. Het substraat bevindt zich binnenin de kamer. De afzetting van dunne films wordt bereikt door het opwekken van een plasma dat chemische reacties aandrijft waarbij materialen met hoge zuiverheid worden gevormd. Veelgebruikte methoden om het plasma te genereren zijn via elektroden of hoogfrequente elektromagnetische golven. Omdat de chemische reacties plaatsvinden in het plasma, kan PECVD een homogene afzetting garanderen over het gewenste afzetgebied. Door de plasma-eigenschappen te variëren, kan het afzetproces worden gestuurd.

Om PECVD-processen te modelleren, kunnen plasmamodellen worden gekoppeld aan veel verschillende soorten fysica, zoals elektromagnetisme, vloeistofstromen en warmteoverdracht. Voor LeydenJar hebben we een waterstofplasma gesimuleerd dat door een microgolf in stand wordt gehouden.

koppelen van plasmafysica aan een microgolfbron.

Het systeem dat werd gemodelleerd bestaat uit een cilindrische coaxiale waveguide die een microgolf draagt. Het plasma wordt gegenereerd in een cilindrisch vacuümvat rond de waveguide.

Om het plasma te modelleren is een model opgezet in COMSOL Multiphysics waarin de microgolf en het plasma zijn gekoppeld. Omdat plasmasimulaties veel rekenkracht vereisen, hebben we ervoor gekozen om een model op te zetten met twee componenten, waarin de microgolven zijn gemodelleerd in een 2D-axisymmetrische component, terwijl het plasma is gemodelleerd als een 1D-axisymmetrische radiale component loodrecht op de waveguide. Met deze opstelling konden de plasma eigenschappen als functie van de afstand tot de waveguide worden verkregen, wat het belangrijkste doel was.

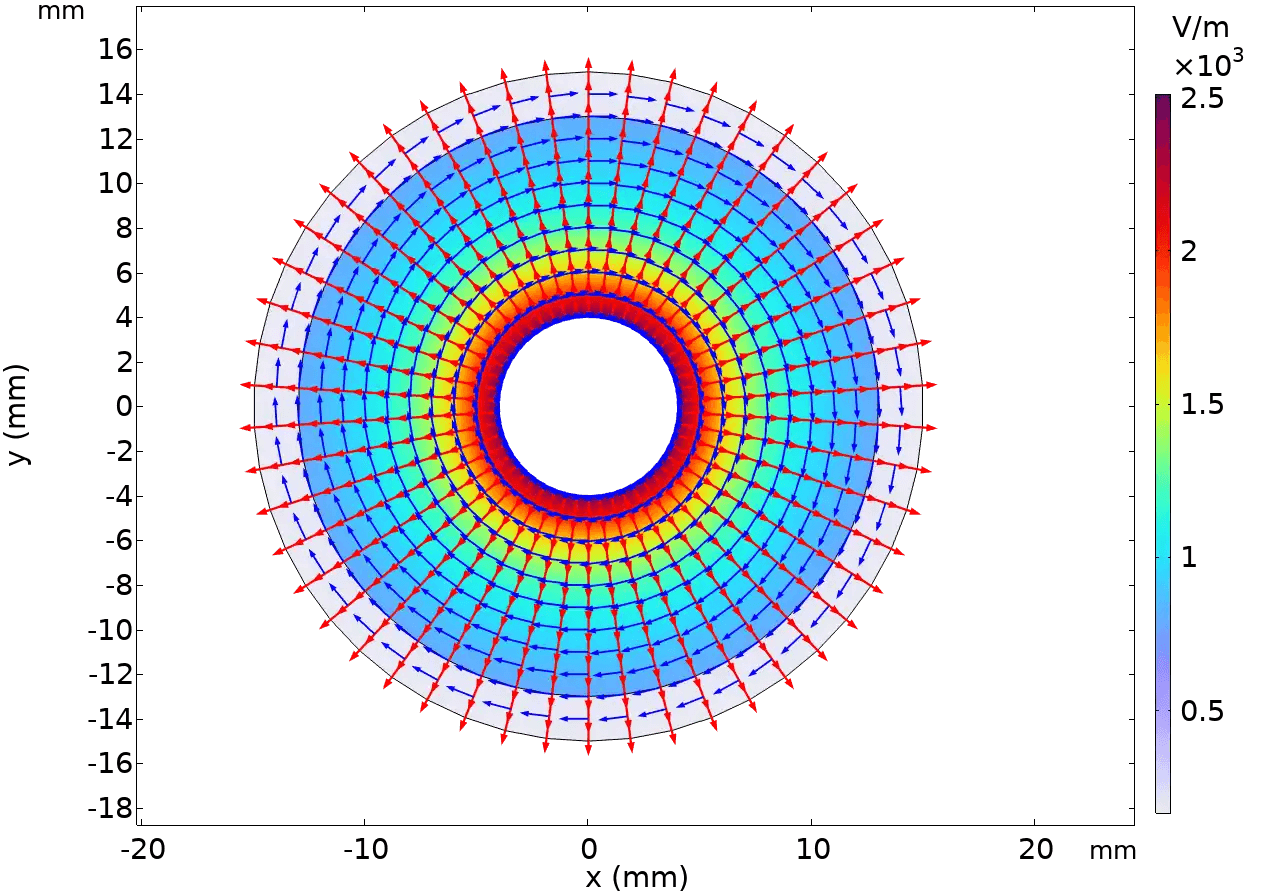
gesimuleerde eigenmodus van een plasma waveguide — Figuur 1 De eigenmodus van de waveguide. De rode pijlen geven de richting van het elektrisch veld aan, de blauwe pijlen de richting van het magneetveld. De kleur is de norm van het elektrisch veld. De richting van de voortplanting van de golf is het scherm in.

Voor het waterstofplasma zijn verschillende H-soorten meegenomen (o.a. H, H*, H**, H⁺, H₂, H₂⁺, H₃⁺). De reactiesnelheden zijn berekend op basis van geïmporteerde doorsneden en reactiecoëfficiënten, evenals de elektronenergieverdelingsfunctie (EEDF). Je kan aannemen dat de EEDF een Maxwell-verdeling is, die alleen een functie is van de elektrontemperatuur, of de EEDF berekenen door de Boltzmann-vergelijking op te lossen. Het berekenen van de EEDF vereist zeer veel rekenkracht in vergelijking met het aannemen van een analytische EEDF, omdat de EEDF dan op elk punt van het raster wordt uitgerekend. Dit kan echter meer inzicht geven in gevallen waarin de EEDF afwijkt van een Maxwelliaanse verdeling.

De voortplanting van de microgolf door de waveguide hangt af van de geleidbaarheid van het plasma. Tegelijkertijd is de microgolf de verwarmingsbron van de elektronen in het plasma, wat invloed heeft op de geleidbaarheid. Door beide componenten te koppelen en de vereiste grootheden uit te wisselen, kan een zelfconsistent model worden opgesteld.

Figurur 2 Elektronendichtheid en -temperatuur als functie van afstand tot de waveguide. De rode lijn geeft de kritische elektronendichtheid aan, waarboven de microgolf zich niet door het plasma kan voortplanten.

resultaten.

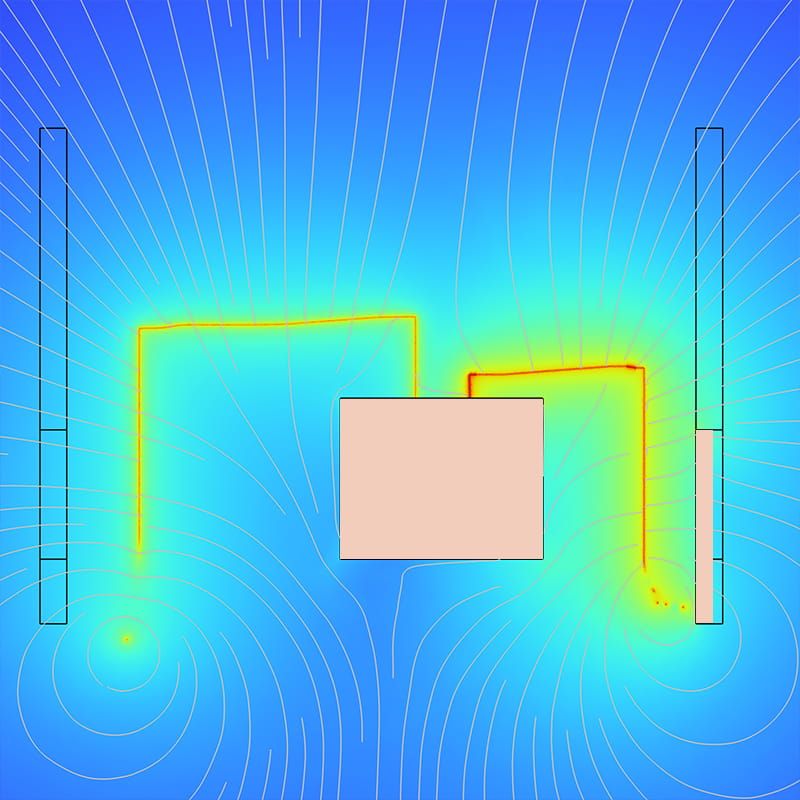
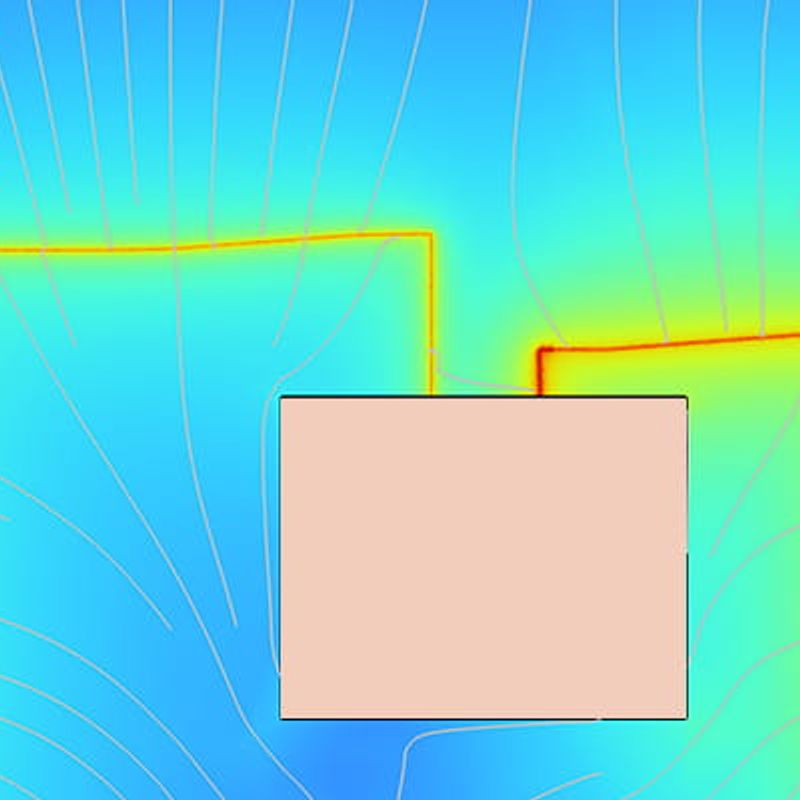
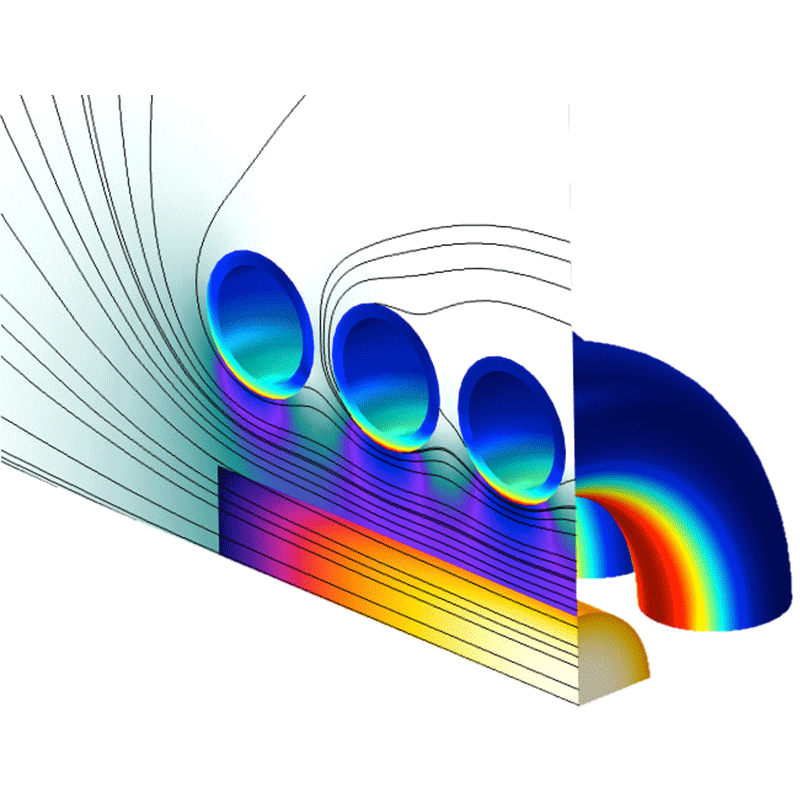
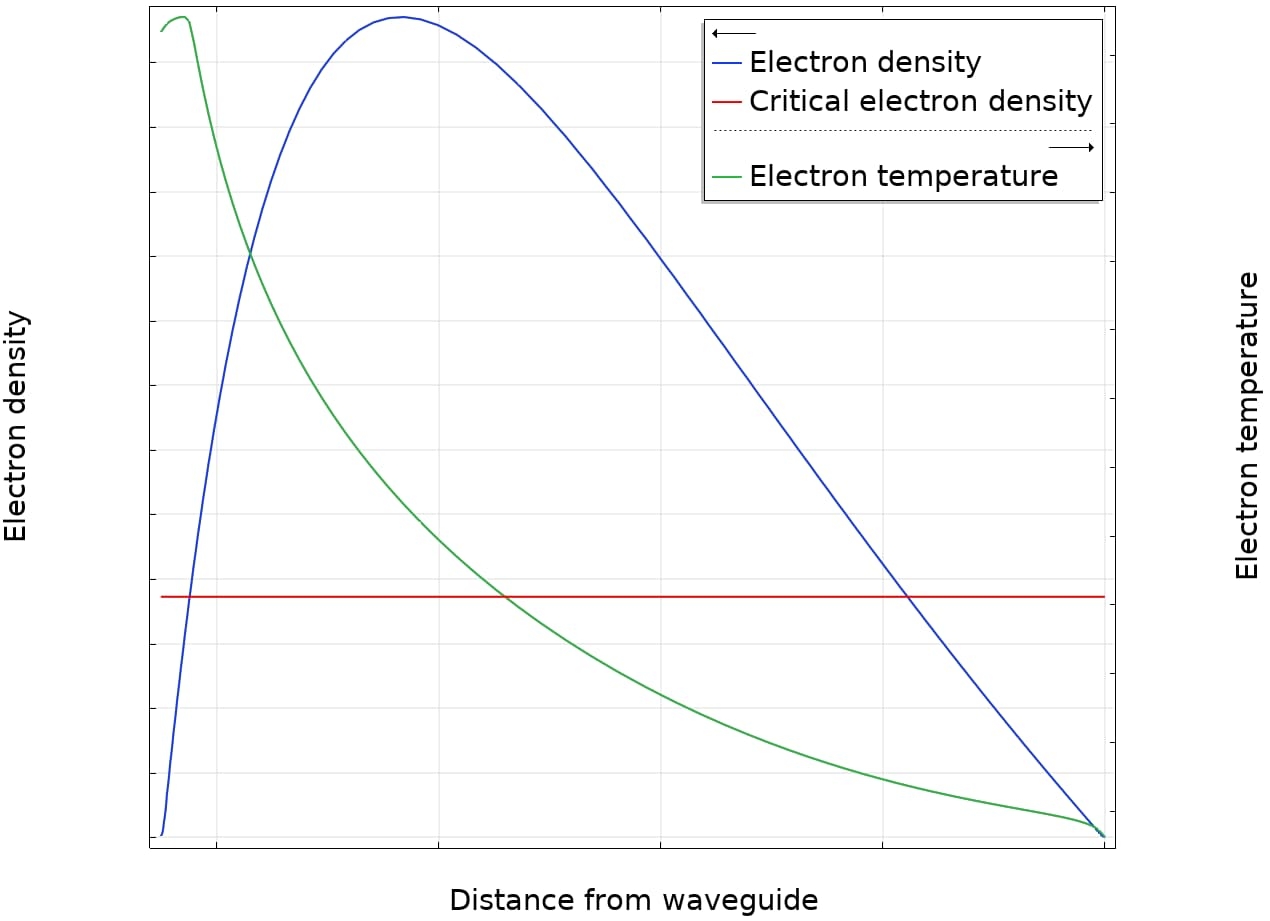
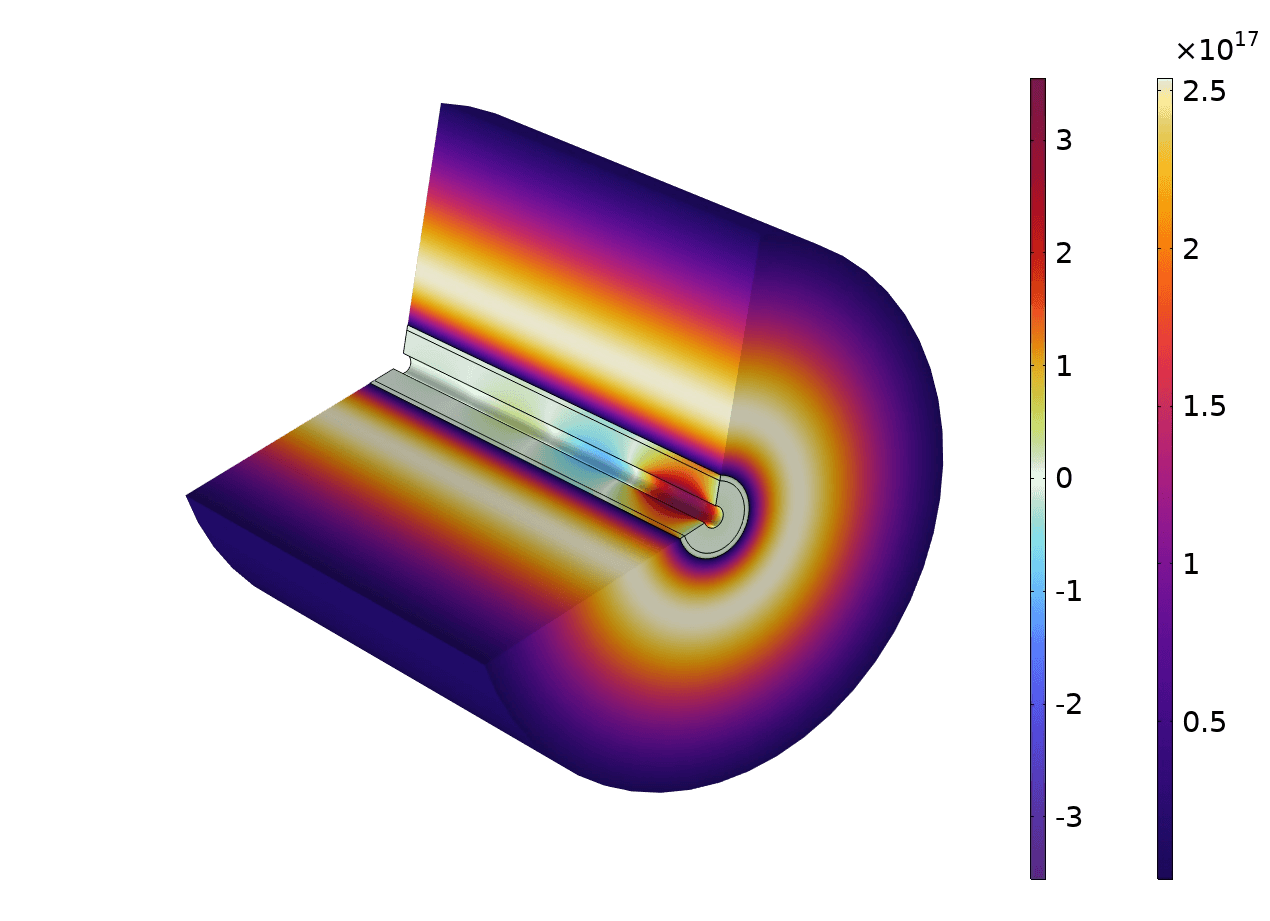
Allereerst werden de eigenmodussen van de waveguide bepaald. Bij de beschouwde frequentie ondersteunt de waveguide slechts één voortplantende eigenmodus, en we hebben aangenomen dat de microgolf in de waveguide zich in deze eigenmodus bevindt, zoals weergegeven in Figuur 1. De microgolf houdt het plasma rond de waveguide in stand. Uit het model konden we informatie over veel verschillende parameters halen. Voorbeelden hiervan zijn de elektronendichtheid en -temperatuur als functie van de afstand tot de waveguide, weergegeven in Figuur 2. De kritische elektronendichtheid is aangegeven met de rode lijn. Als de elektronendichtheid boven deze kritische waarde ligt, kan de microgolf zich niet verder door het plasma voortplanten. Het is in het gebied dicht bij de waveguide, waar de elektronendichtheid gelijk is aan de kritische dichtheid, dat het microgolfvermogen wordt afgezet en waar de elektrontemperatuur het hoogst is.

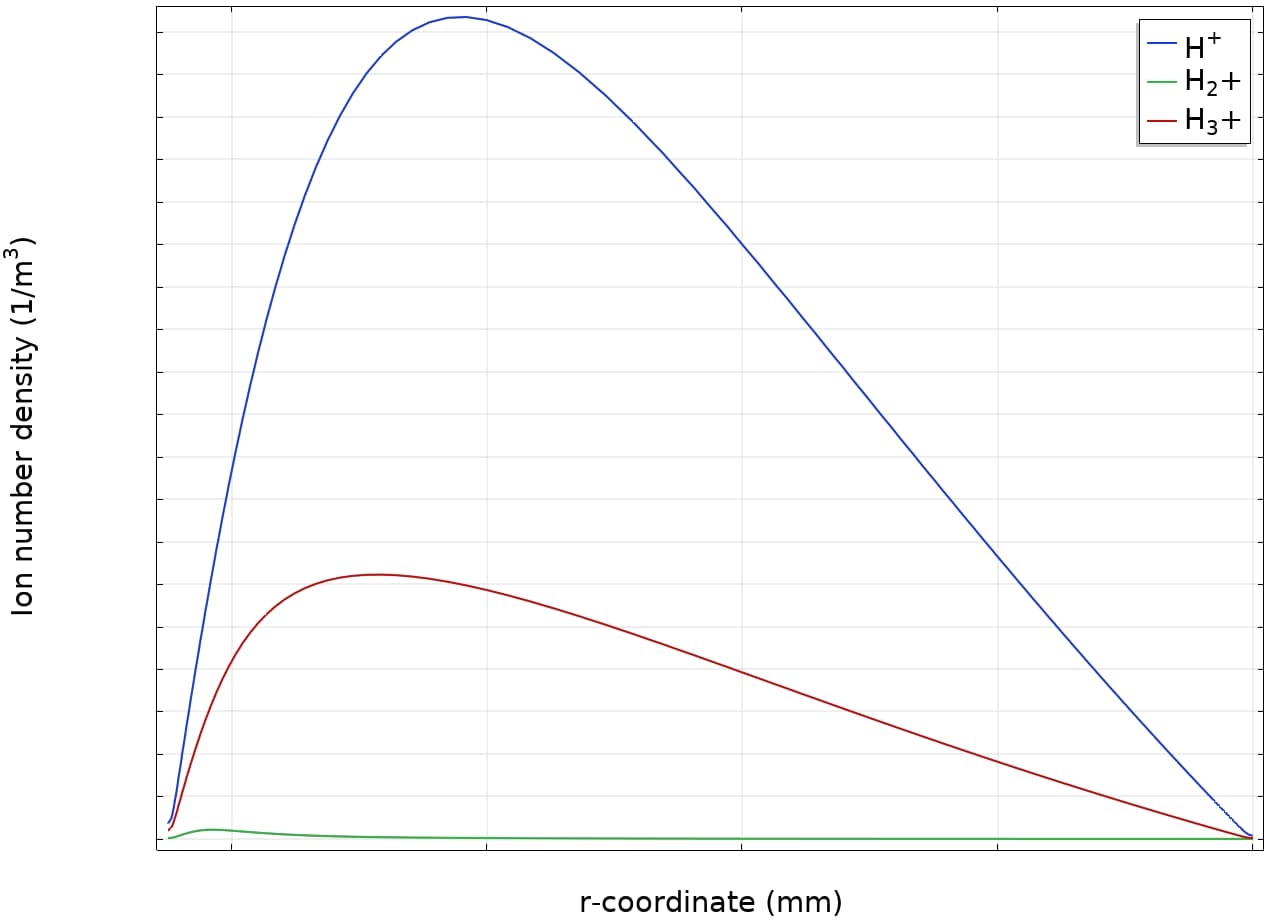
Figuur 3 Dichtheid van de verschillende waterstof ionen, als functie van de afstand tot de waveguide.

Om inzicht te krijgen in een PECVD-proces, wil men doorgaans ook begrijpen hoe ionen of andere reactieve deeltjes zich door het plasma verspreiden. Als voorbeeld toont Figuur 3 de dichtheden van de verschillende waterstofionen als functie van de afstand tot de waveguide. Er zijn (doorgaans) veel meer grootheden van belang die uit een model gehaald kunnen worden, die we hier niet allemaal kunnen laten zien. Enkele voorbeelden zijn reactiesnelheden, het plasmapotentiaal, de EEDF, transportparameters van elektronen en zware deeltjes, en de mate van ionisatie. Indien gewenst kan ook een oppervlaktechemiemodel worden toegevoegd om afzettingssnelheden te berekenen.

Bij LeydenJar hebben onze modellen op drie manieren impact gehad:

Ter illustratie: om de basisprincipes van de plasma-bron te begrijpen.
Ter inspiratie: om experimentele waarnemingen te helpen verklaren.
Voor verdere ontwikkeling: om aannames in vereenvoudigde modellen te toetsen.

Tot slot bieden plasmasimulaties een krachtig hulpmiddel om complex plasma-gedrag en chemische reacties die in een plasma plaatsvinden nauwkeurig te modelleren. Dit maakt diepgaand inzicht mogelijk in zowel fundamentele fysica als praktische toepassingen in halfgeleiderverwerking.